- I'm returning to the Haliburton Forest 50 Miler next weekend, and am a bit apprehensive. Deep breaths. Try to keep it simple. Here's the basic, back-of-the-envelope plan.
First, my taper needs to be
-
and
 .
.
To start the race, my effort should be something like .
.
Oh, and for the uphillsAnd then the downhills (duh)
Naturally, for the second half we'll be looking at

-
Or, alternatively  .
.
(But if I see a bear, I need to run like
 )
)
Happily, my fueling and hydration intake is fool-proof:
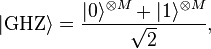
And finally, though it's out of my control I can't help but hope for ideal weather conditions throughout the day:

So really, what could go wrong?

4 comments:
Haha! That is AWESOME. Perfect!
Did you like the GHZ one, GZ? Not sure what H could stand for but you can decide.
Heard it through the grapevine that you had a good run:-) Congratulations!! Now if I can only decipher your above formula(s) for success before October 5th!
Thanks, EJ. The beauty of the formulas is that can mean whatever the heck you want them to. (Unless you're a quantum physicist.)
Post a Comment