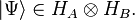- I'm returning to the Haliburton Forest 50 Miler next weekend, and am a bit apprehensive. Deep breaths. Try to keep it simple. Here's the basic, back-of-the-envelope plan.
First, my taper needs to be
-
and
 .
.
To start the race, my effort should be something like .
.
Oh, and for the uphillsAnd then the downhills (duh)
Naturally, for the second half we'll be looking at

-
Or, alternatively  .
.
(But if I see a bear, I need to run like
 )
)
Happily, my fueling and hydration intake is fool-proof:
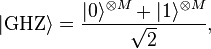
And finally, though it's out of my control I can't help but hope for ideal weather conditions throughout the day:

So really, what could go wrong?